Must you dare into the deep dark nothingness of the liquidity pools, LP? Beware, for a monster named Impermanent Loss will eat you…
To most of us, the concept of an on-chain trading experience without AMMs seems almost unfathomable. But not too long ago, this unfathomable scenario was a reality. Prior to the advent of AMMs, pioneered by Uniswap, DEXs simply mimicked the order book-based exchange model used by centralised exchanges. Very quickly, the developers and users both learned how painful an experience it was trading on-chain. Slow trade execution and high transaction fees are certainly not a recipe for an efficient trading environment.
Thankfully, DeFi saw its 0-to-1 innovation come in the form of AMMs. The very first iteration of an AMM was the constant function market maker. You’ve probably heard of it, the popular x*y=k formula. The basic premise of it is that the pool of reserves for asset x and asset y must always be constant (k). This one simple formula allowed on-chain trading to become significantly faster and cheaper resulting in on-chain trading volume skyrocketing.
As is common in DeFi, new projects often build atop older ones, and Gammaswap is no different. Therefore, to better understand Gammaswap, there’s still a little more that you need to know about Uniswap.
How are prices decided in Uniswap pools?
The price of each asset is determined by dividing the quantity of one asset by the other. For 100 $LINK and 1000 $USDC, the price is determined as 1000 $USD/100 $LINK, which gives $10 USDC/$LINK.
Now, Uniswap relies on another constant (known as the liquidity invariant) when a trade is executed. This invariant is the square root of the product of the two assets in the pool.
LiquidityInvariant(LI) = (ETH ∗ USDC)
Now, let’s suppose that a user plans to exchange X ETH with Y USDC in this liquidity pool. In this case, the liquidity invariant will look something like this (note that the user is supplying ETH to the pool and withdrawing USDC from it),
- = (ETH + X)∗ (USDC − Y )
Thus, as more ETH is added to the liquidity pool, the reserve quantity of USDC decreases. But to keep the pool constant (remember x*y = k), the price of USDC increases to keep the pool balanced. You can better understand this by the following formula,
LI = (ETH + X)∗ (USDC − Y )
⇒
LI2 = (ETH + X)∗ (USDC − Y )
⇒
Y = USDC − [LI2/(ETH + X)]
Thus, as the value of supplied ETH increases, the value of withdrawable Y decreases. In other words, trading of your asset on a pool in Uniswap is inversely proportional to the amount of the asset that you supply to exchange it with.
For this example, we have relied on ETH and USDC. But this can be true for any two assets, a and b. This model is created to ensure that Uniswap replicates the impact the market might have on the exchanging of these tokens.
This is where the prices start getting different to the ones in the prevailing market (especially a centralized exchange). This creates a disparity between the prices of these assets within the market. And this opens up opportunities for…(if you get it you’re a)...

arbitrage! That’s right. Imagine an asset selling for a considerably lower price on Uniswap while it’s selling for higher on other exchanges. You can just buy it on Uniswap, and sell it on other exchanges. To which you might ask…well if that opportunity is available, then wouldn’t these pools remain always balanced?
And you’ll be right.
Arbitrage opportunities generally help keep the price of assets on Uniswap stable - even in the case of a huge transaction.
But where do the reserves in the Uniswap pools come from?

The liquidity pools in Uniswap are generally filled by what are known as liquidity providers (LPs) whose sole purpose is to provide liquidity for two assets in the same ratio. Uniswap charges a transaction fee for trading in its pools - and a percentage of that goes to these LPs in proportion to the liquidity they’ve supplied. In Uniswap V2, users get an LP token in return which represents the share of their liquidity within the pool. The growth of these shares is associated with the liquidity invariant of the pool (LI).
In other words, as the reserves of the tokens grow in the pool, the LI grows, and as the LI grows, the LPs gain more profit from the no. of transactions in the pool.
Liquidity shares of a pool increase when more liquidity providers add liquidity to the pool. However, the existence of multiple LPs in a pool and their withdrawing and deposits of funds has no impact on the profits fellow LPs get from the pool. However, what does affect the price in the pool is the changes in the price that happens in the market (which we’ve already covered above).
The bone of contention: Impermanent Loss

Recall from the previous section that the main value that LPs get from becoming an LP in the first place is the transaction fees that the pool accrues from users who trade in the pool. Now, if we assume that the values of the reserves in the pool are constant, then transaction fees alone will bring in continuously compounding returns for the LPs. For Uniswap V2, the price offered for trades is found by the ratio of the reserves of the assets in the pool.
As you can imagine, when the liquidity pool is hot with trading activity, this ratio continuously changes. The returns from the liquidity pool are proportional to the square root of the price. For more info on how this happens, check out the equations and mathematical calculations here. The nature of the relationship between the returns on the price and the returns you get, the returns from the liquidity pool get skewed in either direction depending on the amount of activity in the pool.
During times of high activity (i.e., a lot of trades being executed → a lot of transaction fees getting accrued), the returns can be much greater than the price at which the liquidity was initially provided by the LP.
So…is this the Impermanent Loss?

Yes and no. Impermanent loss is actually the loss in potential profits that an LP would have gained had they not been providing liquidity to a liquidity pool for a pair of assets. I say potential profits because these profits are relative to the market conditions of the asset in question. This is why AMMs offer trading fees as compensation to LPs for the potential losses that can occur. However, as you would imagine, this compensation is highly correlated to how the market performs.
In a bull market, IL risks can be huge due to high trading activity and high volatility of the assets being traded. Trading fees might/might not be able to offset the IL risks depending on the value of the assets (and a host of other factors) that the LP supplies.
In a bear market, IL risks can be reduced because of the overall reduction in trading activity. However, in that case, the returns are skewed because there is lesser accrual of transaction fees.
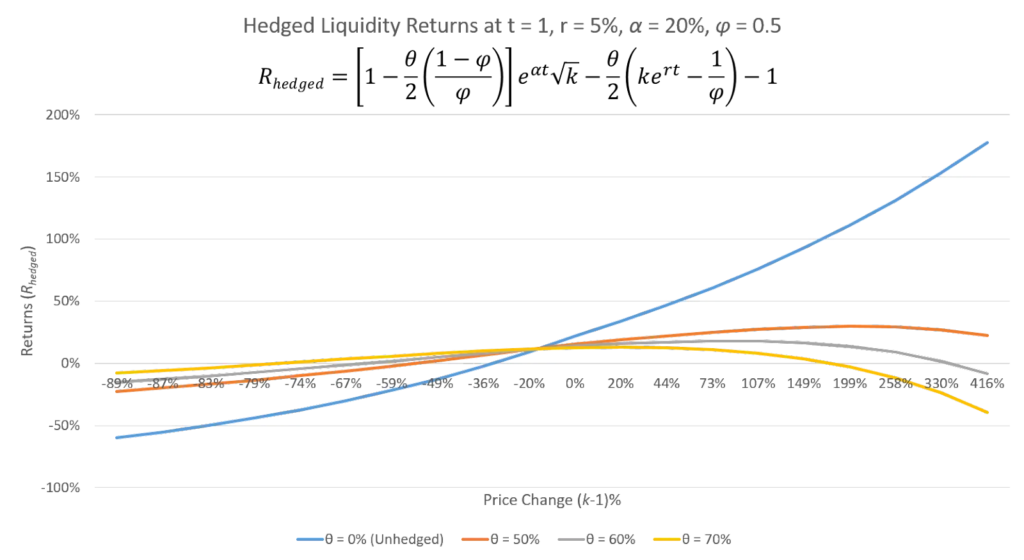
Now, there is a way to hedge the risks that you incur from IL by taking an opposite position of one of the assets you’ve supplied to the liquidity pool. Let’s understand how.
Recall that the price of an asset in Uniswap V2 is the ratio of the two values of the reserves. Thus,
x p =
y
Or,
- = p ∗ y
Here, x is the asset that is priced in relation to the asset, y. And this (x) is the asset whose opposite position we will take to hedge against the risk. The opposite position - in this case - is going to be us shorting x. However, to do that, we’ll need a supply margin. Creating such a short position reduces the variability in returns subject to the market conditions for an LP.
Leveraging Liquidity: Uniswap v3
Uniswap V3 lets users concentrate liquidity within tighter price ranges. In v2, the liquidity you supply gets spread across the entire pool. But in V3, it oscillates between two price ranges that you have the option to choose from. This leverages your initial liquidity provisioning because - as that range becomes more active i.e., heavily traded - your liquidity has a higher chance of earning transaction fees.
Topaze Blue conducted extensive research into the concentrated liquidity but found that there were hardly any cases where users were able to offset the IL associated - even with concentrated liquidity. The assumed offsetting of these risks was not found to be eliminated even from the transaction fees that LPs would accrue. On the contrary, the research yielded that users were better off HODLing their assets as that alone produced greater returns over an extended period of time as opposed to providing liquidity to LPs.
Is Uniswap an options market?
Before we dive deeper into what exactly GammaSwap Labs aims to achieve, it is helpful to understand that your liquidity provisioning positions on Uniswap closely resemble that of an options position. Let’s understand how.
Recall that options (or options contracts) give their holders the right (but not the obligation) to buy or sell an underlying asset at a fixed price. In other words, if you can sell (known as a put) the underlying asset at a higher price than the strike price (or the price at which you bought the options contract) then you make a profit. Conversely, if you can buy (known as a call) the underlying asset at a lower price than the strike price then, too, you make a profit.
What matters is not the price of the option itself, but its ability to make you profit when it expires.
That would further depend on the volatility of the underlying asset. The more volatile the underlying asset, the more chances it gives the holder of the option to be profitable. Another crucial thing to understand here is the premium that a holder has to pay to get the underlying asset. For them, this volatility will be a crucial deciding factor for whether they should get the contract. One way to track that would be to look at the historical volatility of that asset.
Since this volatility is highly subject to a multitude of factors, an options trader generally hedges their position via something known as delta hedging.
What is Delta?
Delta is one of the Greek symbols that are used to define the risks involved with options. These symbols are used to balance portfolios subject to various risks with the options contracts. Delta, specifically, reflects the relationship between the change in the price of an option and the change in the price of the underlying asset. Delta hedging works by going long or short the underlying asset to balance risks.
The risk that the trader takes, in this case, is of the moving delta - which reflects the moves of the underlying asset. To counter this, traders adopt what is known as dynamic hedging i.e., they manage their delta exposure according to the real-time changes in the underlying asset’s price. This is done to stay “delta-neutral”.
But wait…how is delta hedging related to Uniswap?

Because this delta-hedging is also what Uniswap is doing with its liquidity pools. Let’s understand how.
Depending on which asset’s price moves, it dynamically opens a long position on that asset. For a liquidity pool with assets A and B, if the former’s price falls then Uniswap increases the long exposure to that asset.
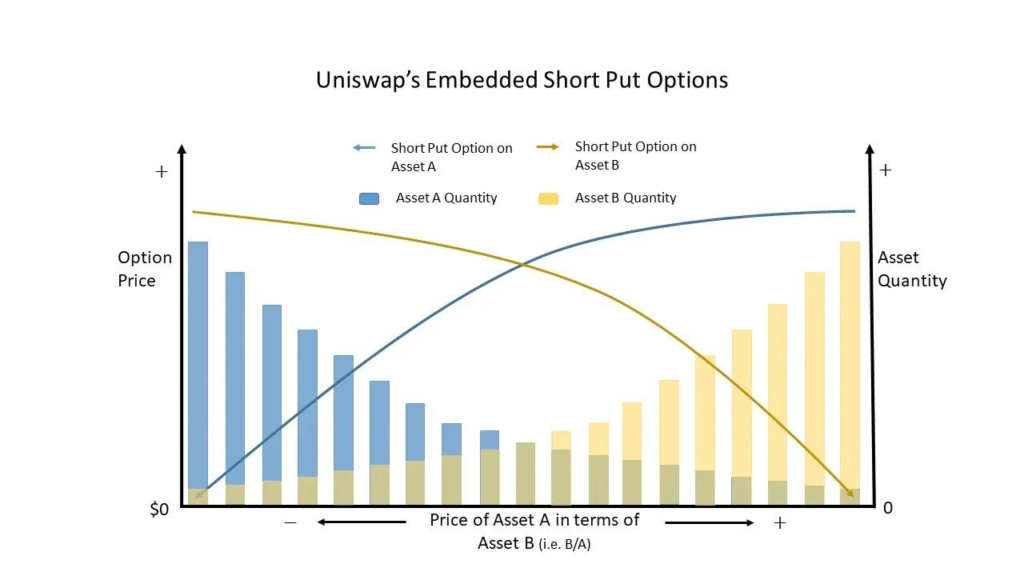
Thus the yield that users get when providing liquidity to AMMs (especially Uniswap) is coming from the implied volatility of the underlying asset. This is highly subject to the prevailing market conditions. For instance, in an analysis conducted by GammaSwap Labs, they found that the implied volatility is worth the risk during certain periods of providing liquidity. But this risk becomes futile as the pool scales. This is especially true for Uniswap V3: while even with leveraged liquidity, the fees that the pool earns gets divided into lesser participants, it tends towards becoming a more active investment strategy than being a passive one.
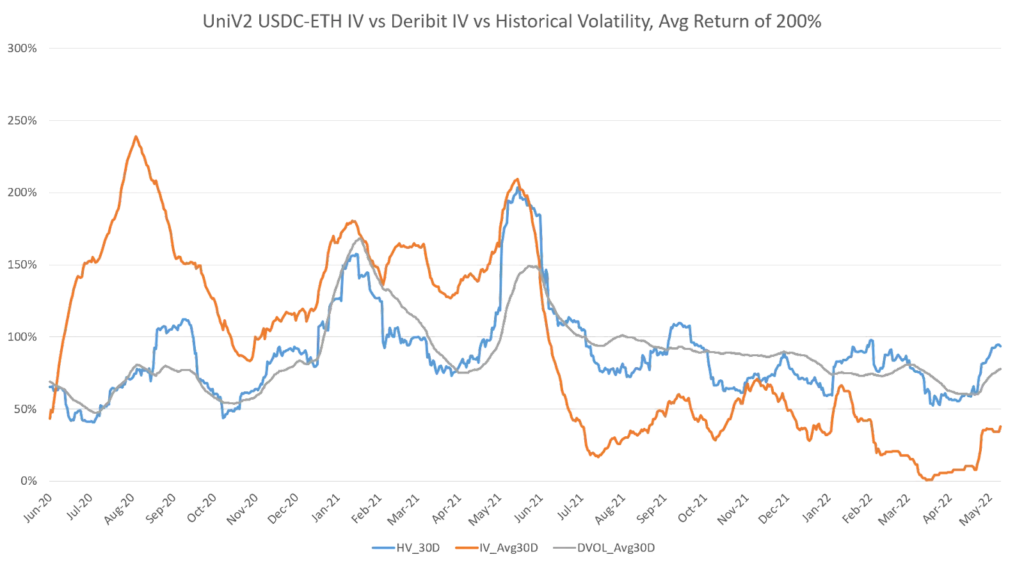
We must also understand that a lot of the gains that a user makes from providing liquidity also come from the utilization of the liquidity pool in the first place. The more trading activity on the pool, the higher you get more from the transaction fees that the pool accrues. However, the very cyclical nature of markets renders the returns very volatile.
The Dilemma: to LP or not to LP
For any liquidity provider, a key enticing factor for providing their liquidity to a pool is the value they are able to generate via transaction fees. Add to this the price appreciation that might happen in the native asset that they have used to provide liquidity. However, as we have seen in previous sections, the risk of IL greatly off-set the ability of an LP to generate consistently profitable returns across various bull and bear cycles.
Liquidity pools are an extremely crucial part of DeFi: currently, Uniswap alone processes over $620M worth of transactions every day. Add to this the daily volume processed by the remaining top 4 AMMs which sits around $420M and we already see over $1B of volume being needed to process the vast number of trades happening across the entire ecosystem.
<div style="position: relative; width: 100%; padding-bottom: 56.25%;">
<iframe
style="position:absolute; width:100%; height:100%;"
src="https://www.getyarn.io/yarn-clip/067338bd-7431-46bd-8f0d-10dca4f548c1/embed?autoplay=false&responsive=true"
frameborder="0"
></iframe>
</div>
There is ABSOLUTELY no contesting the fact that liquidity pools are the engines powering all of DeFi. If liquidity providers (the engine runners) aren’t profitable in the long run from their liquidity provisioning, then it is a problem.
Introducing GammaSwap Labs
By providing liquidity via GammaSwap, a user is effectively shorting Gamma, thereby selling volatility. This can be considered a pseudo-hedge in a way because the user is now able to earn borrow fees from those longing volatility.
When depositing via GammaSwap, users get a chance to short their liquidity on an AMM by borrowing from the same liquidity pool.
This is how the LPs turn the infamous Impermanent Loss (IL) into the revered Impermanent Gain (IG).

But wait…where does the ability to borrow from an AMM come from? You see, when you borrow liquidity from GammaSwap, you do it in one of the reserve tokens, which are worth more than the LP tokens (that get burned). These reserve tokens are held as collateral.
Thus, the initial LPs who provided their liquidity to GammaSwap get:
trading fees from AMMs + borrower fees
GammaSwap’s smart contracts keep track of the associated yields with the loans that they lend and so on.
From the outside, GammaSwap Labs functions exactly the same as any other liquidity pool.
Liquidity providers provide their liquidity to GammaSwap, which in turn deposits that to the AMMs. In return, the LPs get the standard LP token - just as they would get it from AMMs. When the liquidity provider wants to exit their position from GammaSwap, they simply return the LP tokens and are given back the native tokens they deposited + the yield they have generated from providing liquidity. Providing liquidity via GammaSwap to CFMMs helps the user get yields that are always greater than or equivalent to what they would get from the underlying liquidity pool (excluding liquidity mining incentives).
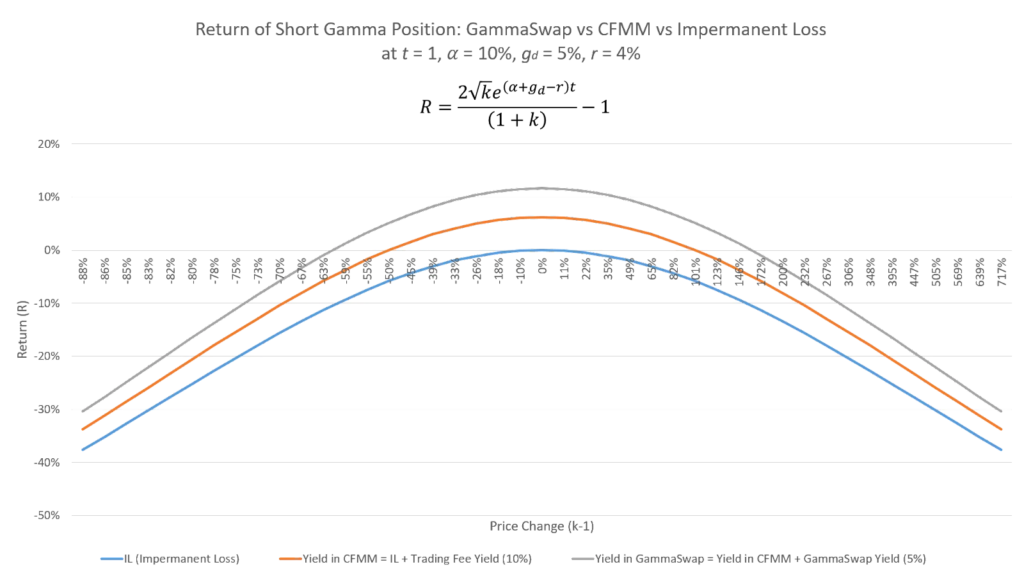
To ensure that the loans that are being borrowed out of GammaSwap Labs are secure, the borrower has to overcollateralize them. If they fall below a certain value, then a third party can liquidate the loan and it gets to keep a percentage of the collateral.
GammaSwap doesn’t rely on oracles
Most lending/borrowing markets rely on oracles to fetch the prices of the assets. These protocols are generally not reliant on CFMMs because of the risks of flash-loan attacks that can be induced by manipulating the prices of assets on CFMMs. That risk doesn’t apply to GammaSwap Labs because they use the liquidity invariant to track borrowed positions. Since this is not influenced by the changes in the price of the underlying tokens in the AMM, the typical flash loan attacks do not affect the borrowers’ positions.
Thus, GammaSwap does not need to rely on any third-party oracles in the first place.
GammaSwap might make AMM charge a low-to-no fee
If LPs are able to take the opposite bet of an LP and turn their IL to IG, then the AMM do not need to charge the trading fees in the first place. Thus, GammaSwap enables a potential no-fee trading marketplace for AMMs in the future.
GammaSwap Labs’ Community
At the moment, their community is limited to people on Twitter and Discord, with a combined social community of over 43K members already! Their Discord community alone has about 23.7K members. They also have a test net that is available that users can use to test out the entire product.
You can head over to their Discord, and participate in the Closed Beta Testnet on Goerli. Note that it is only currently live for Degen Score Beacon Holders. To participate in their testnet, head over to their #testnet-guide channel, use the Goerli faucet to get funds, and start testing at https://app.gammaswap.com/. The GammaSwap team also responds very actively to any questions and/or product-related feedback you might have on Discord.
GammaSwap Lab’s Team
GammaSwap Labs’ team consists of possibly some of the biggest gigabrains in the industry. With three highly technical co-founders (Devin Goodkin, Daniel Alcarraz, and Roberto Martin) each with extensive experience across both TradFi and Web3 products, the team seems to have an incomparable edge in the industry.
They also recently conducted a fundraising round and have raised a total sum of $1.7M from Modular Capital, Space Whale Capital, Ouroboros Capital and two of the GMX co-founders including Coinflip and Quat. Quat is also an advisor for the economic aspects of GammaSwap’s product and tokenomics. You can find the entire list of their backers here.
Concluding Thoughts
GammaSwap Labs seems like a very promising project. They are tackling a fundamental problem in crypto, and if they are successful, we will see a huge pain point that exists for liquidity providers being solved. Once it ships on mainnet in Q1, 2023 it would be great to see the interest from fellow DeFi protocols - especially the likes of Uniswap and Curve. Imagine if all the LPs could convert their Impermanent Loss to Impermanent Gain - this will bring in a lot of capital not just from retail but also from institutions!













